Bir hücresel otomat (pl. cellular automata, kısaltması CA), otomata teorisinde incelenen ayrı bir hesaplama modelidir. Hücresel otomatlar aynı zamanda hücresel boşluklar, mozaikleme otomatları, homojen yapılar, hücresel yapılar, mozaikleme yapıları ve yinelemeli diziler olarak da adlandırılır.[2] Hücresel otomatlar, fizik, teorik biyoloji ve mikro yapı modelleme dahil olmak üzere çeşitli alanlarda uygulama bulmuştur.
Hücresel bir otomat, her biri açık ve kapalı gibi (birleştirilmiş bir harita kafesinin aksine) sonlu sayıda durumdan birinde olan düzenli bir hücre ızgarasından oluşur. Izgara, herhangi bir sonlu sayıda boyutta olabilir. Her hücre için, belirtilen hücreye göre komşuluğu adı verilen bir hücre kümesi tanımlanır. Her hücre için bir durum atanarak bir başlangıç durumu (zaman t = 0) seçilir. Her hücrenin yeni durumunu, hücrenin mevcut durumu ve hücrelerin durumları açısından belirleyen sabit bir kurala (genellikle matematiksel bir işlev)[3] göre yeni bir nesil yaratılır (t’yi 1 birim ilerleten). mahallesinde. Tipik olarak, hücrelerin durumunu güncelleme kuralı her hücre için aynıdır ve zaman içinde değişmez ve stokastik hücresel otomat ve eşzamansız hücresel otomat gibi istisnalar bilinmesine rağmen aynı anda tüm ızgaraya uygulanır[4] .
Konsept ilk olarak 1940’larda Stanislaw Ulam ve John von Neumann tarafından Los Alamos Ulusal Laboratuvarı’nda çağdaşken keşfedildi. 1950’ler ve 1960’lar boyunca bazıları tarafından incelenirken, konuya olan ilgi akademi sınırlarının ötesine ancak 1970’lere ve Conway’in iki boyutlu bir hücresel otomat olan Game of Life’ına kadar ulaştı. 1980’lerde Stephen Wolfram, tek boyutlu hücresel otomatlar veya kendisinin temel hücresel otomatlar dediği şey üzerine sistematik bir çalışma yürüttü; araştırma asistanı Matthew Cook, bu kurallardan birinin Turing-complete olduğunu gösterdi.
Wolfram tarafından ana hatları çizilen hücresel otomatların birincil sınıflandırmaları birden dörde kadar numaralandırılmıştır. Bunlar sırasıyla, örüntülerin genellikle homojenliğe stabilize olduğu otomatlar, örüntülerin çoğunlukla kararlı veya salınımlı yapılara evrildiği otomatlar, örüntülerin görünüşte kaotik bir tarzda geliştiği otomatlar ve örüntülerin son derece karmaşık hale geldiği ve yıllarca sürebildiği otomatlardır. uzun bir süre, istikrarlı yerel yapılarla. Bu son sınıfın, hesaplama açısından evrensel olduğu veya bir Turing makinesini simüle edebildiği düşünülmektedir. Özel hücresel otomata türleri tersine çevrilebilir, burada yalnızca tek bir konfigürasyon doğrudan bir sonrakine yol açar ve totalistik, burada tek tek hücrelerin gelecekteki değeri yalnızca bir grup komşu hücrenin toplam değerine bağlıdır. Hücresel otomatlar, biyolojik ve kimyasal olanlar da dahil olmak üzere çeşitli gerçek dünya sistemlerini simüle edebilir.
Genel bakış
İki boyutlu bir hücresel otomatı simüle etmenin bir yolu, hücrelerin izlemesi için bir dizi kuralla birlikte sonsuz bir grafik kağıdı kullanmaktır. Her kareye “hücre” denir ve her hücrenin siyah ve beyaz olmak üzere iki olası durumu vardır. Bir hücrenin komşuluğu, yakındaki, genellikle bitişik hücrelerdir. En yaygın iki mahalle türü, von Neumann mahallesi ve Moore mahallesidir.[5] Adını kurucu hücresel otomat teorisyeninden alan ilki, birbirine dik dört bitişik hücreden oluşur.[5] İkincisi, von Neumann mahallesini ve çapraz olarak bitişik dört hücreyi içerir.[5] Böyle bir hücre ve onun Moore mahallesi için 512 (= 2 üzeri 9) olası örüntü vardır. 512 olası modelin her biri için, kural tablosu bir sonraki zaman aralığında merkez hücrenin siyah mı yoksa beyaz mı olacağını belirtir. Conway’s Game of Life, bu modelin popüler bir versiyonudur. Diğer bir yaygın komşuluk türü, her ortogonal yönde en yakın iki hücreyi içeren ve toplam sekiz hücreyi içeren genişletilmiş von Neumann komşuluğudur.[5] Böyle bir kurallar sistemi için genel denklem kks’dir; burada k, bir hücre için olası durumların sayısıdır ve s, hücrenin bir sonraki durumunu belirlemek için kullanılan komşu hücrelerin sayısıdır (hesaplanacak hücre dahil).[6] Böylece, bir Moore komşuluğuna sahip iki boyutlu sistemde, mümkün olan toplam otomata sayısı 2 üzeri 2 üzeri 9 veya 1.34 × 10 üzeri 154 olacaktır.
Diğer durumlardaki sınırlı sayıda hücre dışında, genellikle evrendeki her hücrenin aynı durumda başladığı varsayılır; durum değerlerinin atanmasına konfigürasyon denir.[7] Daha genel olarak, bazen evrenin periyodik bir modelle kaplı olarak başladığı ve yalnızca sınırlı sayıda hücrenin bu modeli ihlal ettiği varsayılır. İkinci varsayım, tek boyutlu hücresel otomatlarda yaygındır.
Bir simit, bir toroidal şekil
Hücresel otomatlar genellikle sonsuz değil sonlu bir ızgara üzerinde simüle edilir. İki boyutta, evren sonsuz bir düzlem yerine bir dikdörtgen olurdu. Sonlu ızgaralarla ilgili bariz sorun, kenarlardaki hücrelerin nasıl ele alınacağıdır. Nasıl ele alındıkları, ızgaradaki tüm hücrelerin değerlerini etkiler. Olası bir yöntem, bu hücrelerdeki değerlerin sabit kalmasına izin vermektir. Diğer bir yöntem ise bu hücreler için farklı komşuluk tanımlamalarıdır. Daha az komşuları olduğu söylenebilir, ancak o zaman kenarlarda bulunan hücreler için de yeni kurallar tanımlamak gerekir. Bu hücreler genellikle toroidal bir düzende ele alınır: üstten çıkıldığında alttaki ilgili konuma gelir ve soldan çıkıldığında sağdan girer. (Bu, esas olarak sonsuz bir periyodik döşemeyi simüle eder ve kısmi diferansiyel denklemler alanında bazen periyodik sınır koşulları olarak adlandırılır.) Bu, bir tüp oluşturmak için dikdörtgenin sol ve sağ kenarlarını bantlamak, ardından üstünü bantlamak olarak görselleştirilebilir. ve bir simit (çörek şekli) oluşturmak için tüpün alt kenarları. Diğer boyutlardaki evrenler de benzer şekilde ele alınır. Bu, komşuluklarla ilgili sınır problemlerini çözer, ancak başka bir avantajı da modüler aritmetik fonksiyonlar kullanılarak kolayca programlanabilmesidir. Örneğin, aşağıdaki örneklerdeki gibi 1 boyutlu bir hücresel otomatta, bir xit hücresinin komşuluğu {xi−1t−1, xit−1, xi+1t−1}’dir, burada t zaman adımıdır (dikey), ve i, bir nesildeki dizindir (yatay).
Tarihi
Stanislaw Ulam, 1940’larda Los Alamos Ulusal Laboratuvarı’nda çalışırken, modeli olarak basit bir kafes ağı kullanarak kristallerin büyümesini inceledi.[8] Aynı zamanda, Ulam’ın Los Alamos’taki meslektaşı John von Neumann, kendi kendini kopyalayan sistemler sorunu üzerinde çalışıyordu.[9] Von Neumann’ın ilk tasarımı, bir robotun başka bir robot inşa etmesi fikri üzerine kuruldu. Bu tasarım kinematik model olarak bilinir.[10][11] Bu tasarımı geliştirirken, von Neumann kendi kendini kopyalayan bir robot yapmanın büyük zorluğunu ve robota kendi kopyasını inşa edeceği bir “parçalar denizi” sağlamanın büyük maliyetini fark etti. Neumann, 1948’deki Hixon Sempozyumu için “Otomata’nın genel ve mantıksal teorisi” başlıklı bir makale yazdı.[9] Ulam, indirgemeci bir kendini çoğaltma modeli oluşturmak için ayrı bir sistem kullanmayı öneren kişiydi.[12][13] Nils Aall Barricelli, bu yapay yaşam modellerinin ilk keşiflerinin çoğunu gerçekleştirdi.
John von Neumann, Los Alamos kimlik kartı
Ulam ve von Neumann, 1950’lerin sonlarında sıvı hareketini hesaplamak için bir yöntem geliştirdi. Yöntemin itici konsepti, bir sıvıyı ayrı birimlerden oluşan bir grup olarak ele almak ve her birinin hareketini komşularının davranışlarına göre hesaplamaktı.[14] Böylece ilk hücresel otomata sistemi doğdu. Ulam’ın kafes ağı gibi, von Neumann’ın hücresel otomatları da algoritmik olarak uygulanan kendi kopyalayıcısıyla iki boyutludur. Sonuç, küçük bir mahalleye (yalnızca dokunan hücreler komşudur; von Neumann’ın hücresel otomatasında yalnızca ortogonal hücreler) ve hücre başına 29 durumla hücresel bir otomat içinde çalışan evrensel bir kopyalayıcı ve oluşturucuydu.[15] Von Neumann, bunu yapabilen 200.000 hücreli bir konfigürasyon tasarlayarak, belirli bir modelin verili hücresel evrende kendisinin sonsuz kopyalarını oluşturacağına dair bir varoluş kanıtı verdi.[15] Bu tasarım mozaikleme modeli olarak bilinir ve von Neumann evrensel yapıcısı olarak adlandırılır.[16]
Yine 1940’larda Norbert Wiener ve Arturo Rosenblueth, hücresel otomatın bazı özelliklerine sahip bir uyarılabilir ortam modeli geliştirdiler.[17] Spesifik motivasyonları, kalp sistemlerindeki impuls iletiminin matematiksel tanımıydı. Ancak modelleri hücresel bir otomat değildir çünkü sinyallerin yayıldığı ortam süreklidir ve dalga cepheleri eğrilerdir.[17][18] Uyarılabilir ortamın gerçek bir hücresel otomat modeli, 1978’de J. M. Greenberg ve S. P. Hastings tarafından geliştirildi ve incelendi; bkz. Greenberg-Hastings hücresel otomat. Wiener ve Rosenblueth’un orijinal çalışması birçok kavrayış içermektedir ve kardiyak aritmi ve uyarılabilir sistemler üzerine modern araştırma yayınlarında alıntılanmaya devam etmektedir.[19]
1960’larda, hücresel otomatlar belirli bir dinamik sistem türü olarak incelendi ve ilk kez sembolik dinamiklerin matematiksel alanıyla bağlantı kuruldu. 1969’da Gustav A. Hedlund, hücresel otomatların matematiksel çalışması için hala ufuk açıcı bir makale olarak kabul edilen bu bakış açısını[20] takip eden birçok sonucu derledi. En temel sonuç, Curtis-Hedlund-Lyndon teoreminde, hücresel otomatların küresel kuralları kümesinin, geçiş uzaylarının sürekli endomorfizmleri kümesi olarak karakterizasyonudur.
1969’da Alman bilgisayar öncüsü Konrad Zuse, Evrenin fiziksel yasalarının doğası gereği ayrık olduğunu ve tüm evrenin tek bir hücresel otomat üzerindeki deterministik bir hesaplamanın çıktısı olduğunu öne süren Hesaplama Alanı adlı kitabını yayınladı; “Zuse’nin Teorisi”, dijital fizik adı verilen çalışma alanının temeli oldu.[21]
Ayrıca 1969’da bilgisayar bilimcisi Alvy Ray Smith, CA’nın genel bir bilgisayar sınıfı olarak ilk matematiksel tedavisi olan Hücresel Otomata Teorisi üzerine bir Stanford Doktora tezini tamamladı. Bu tezden pek çok makale geldi: Çeşitli şekillerdeki mahallelerin denkliğini, bir Moore’u bir von Neumann mahallesine nasıl indirgeyeceğinizi veya herhangi bir mahalleyi bir von Neumann mahallesine nasıl indirgeyeceğinizi gösterdi.[22] İki boyutlu CA’nın evrensel hesaplama olduğunu kanıtladı, 1 boyutlu CA’yı tanıttı ve basit komşuluklarda bile bunların da evrensel hesaplama olduğunu gösterdi.[23] Yapı evrenselliğinin (ve dolayısıyla kendi kendini yeniden üreten makinelerin) karmaşık von Neumann kanıtını, 1 boyutlu bir CA’da hesaplama evrenselliğinin bir sonucuna nasıl dahil edeceğini gösterdi.[24] Von Neumann’ın CA hakkındaki kitabının Almanca baskısına giriş olarak tasarlanan, çoğu yazar tarafından on yıldan fazla bir süredir birçok ülkede birçok yazarın makalelerine yapılan düzinelerce referansla birlikte, modern CA araştırmacıları tarafından genellikle göz ardı edilen bir alan araştırması yazdı. [25]
1970’lerde, Game of Life adlı iki durumlu, iki boyutlu bir hücresel otomat, özellikle erken bilgisayar topluluğu arasında yaygın olarak bilinir hale geldi. John Conway tarafından icat edilen ve Martin Gardner tarafından bir Scientific American makalesinde[26] popüler hale getirilen kuralları aşağıdaki gibidir:
İkiden az canlı komşusu olan herhangi bir canlı hücre, sanki yetersiz nüfustan kaynaklanıyormuş gibi ölür.
İki veya üç canlı komşusu olan herhangi bir canlı hücre, bir sonraki nesle aktarılır.
Üçten fazla canlı komşusu olan herhangi bir canlı hücre, aşırı nüfus nedeniyle ölür.
Tam olarak üç canlı komşusu olan herhangi bir ölü hücre, sanki üreme yoluyla canlı bir hücreye dönüşür.
Sadeliğine rağmen, sistem görünür rastgelelik ve düzen arasında dalgalanan etkileyici bir davranış çeşitliliği elde eder. Game of Life’ın en belirgin özelliklerinden biri, planörlerin, esas olarak kendilerini ızgara boyunca hareket ettiren hücre düzenlemelerinin sık sık ortaya çıkmasıdır. Otomatı, planörlerin hesaplamalar yapmak için etkileşimde bulunacağı şekilde düzenlemek mümkündür ve uzun çabalardan sonra, Game of Life’ın evrensel bir Turing makinesini taklit edebileceği gösterilmiştir.[27] Büyük ölçüde eğlence konusu olarak görülüyordu ve 1970’lerin başında Game of Life’ın özelliklerini ve ilgili birkaç kuralı araştırmak dışında çok az takip çalışması yapıldı.
Stephen Wolfram, doğada Termodinamiğin İkinci Kanunu’nu ihlal ederek karmaşık kalıpların nasıl oluştuğunu düşündükten sonra 1981’in ortalarında bağımsız olarak hücresel otomatlar üzerinde çalışmaya başladı.[29] Araştırmaları, başlangıçta sinir ağları gibi modelleme sistemlerine olan ilgiden kaynaklandı.[29] Haziran 1983’te temel hücresel otomatları (özellikle Kural 30) araştıran Review of Modern Physics’te ilk makalesini yayınladı.[2][29] Bu basit kuralların davranışlarının beklenmedik karmaşıklığı, Wolfram’ın doğadaki karmaşıklığın benzer mekanizmalardan kaynaklanabileceğinden şüphelenmesine yol açtı.[29] Ancak araştırmaları, hücresel otomatların sinir ağlarını modellemede zayıf olduğunu fark etmesine yol açtı.[29] Ek olarak, bu dönemde Wolfram içsel rastgelelik ve sayısal indirgenemezlik kavramlarını formüle etti[30] ve kural 110’un evrensel olabileceğini öne sürdü – bu daha sonra Wolfram’ın araştırma asistanı Matthew Cook tarafından 1990’larda kanıtlandı.[31]
Sınıflandırma
Wolfram, A New Kind of Science’ta ve 1980’lerin ortalarından kalma çeşitli makalelerde, davranışlarına bağlı olarak hücresel otomatların ve diğer birkaç basit hesaplama modelinin bölünebileceği dört sınıf tanımladı. Hücresel otomata ile ilgili daha önceki çalışmalar, belirli kurallar için model türlerini belirlemeye çalışma eğilimindeyken, Wolfram’ın sınıflandırması, kuralların kendilerini sınıflandırmaya yönelik ilk girişimdi. Karmaşıklık sırasına göre sınıflar şunlardır:
Sınıf 1: Neredeyse tüm başlangıç kalıpları hızlı bir şekilde istikrarlı, homojen bir duruma dönüşür. İlk modeldeki herhangi bir rastgelelik kaybolur.[32]
Sınıf 2: Neredeyse tüm başlangıç modelleri, hızlı bir şekilde kararlı veya salınımlı yapılara dönüşür. İlk modeldeki rastgeleliğin bir kısmı filtrelenebilir, ancak bir kısmı kalır. İlk modeldeki yerel değişiklikler yerel kalma eğilimindedir.[32]
Sınıf 3: Neredeyse tüm başlangıç kalıpları sözde rastgele veya kaotik bir şekilde gelişir. Ortaya çıkan herhangi bir sabit yapı, çevredeki gürültü tarafından hızla yok edilir. İlk modeldeki yerel değişiklikler süresiz olarak yayılma eğilimindedir.[32]
Sınıf 4: Neredeyse tüm ilk kalıplar, uzun süreler boyunca hayatta kalabilen yerel yapıların oluşumu ile karmaşık ve ilginç şekillerde etkileşime giren yapılara dönüşür.[33] Nihai sonuç, Sınıf 2 tipi kararlı veya salınan yapılar olabilir, ancak bu duruma ulaşmak için gereken adım sayısı, ilk model nispeten basit olsa bile çok fazla olabilir. İlk modeldeki yerel değişiklikler süresiz olarak yayılabilir. Wolfram, hepsi olmasa da birçok sınıf 4 hücresel otomatın evrensel hesaplama yeteneğine sahip olduğunu tahmin etti. Bu, Kural 110 ve Conway’in Hayat Oyunu için kanıtlanmıştır.
Bu tanımlar doğası gereği nitelikseldir ve yorum için biraz yer vardır. Wolfram’a göre, “… hemen hemen her genel sınıflandırma şemasında, bir tanım tarafından bir sınıfa ve başka bir tanım tarafından başka bir sınıfa atanan durumlar kaçınılmaz olarak vardır. Hücresel otomatlarda da durum böyledir: ara sıra kurallar vardır… bir sınıfın bazı özelliklerini ve diğerinin bazı özelliklerini gösterir.”[34] Wolfram’ın sınıflandırması deneysel olarak hücresel otomata çıktılarının sıkıştırılmış uzunluklarının bir kümelenmesiyle eşleştirilmiştir.[35]
Wolfram’ın sınıflandırmasından esinlenerek, hücresel otomatları resmi olarak titiz sınıflarda sınıflandırmak için birkaç girişimde bulunuldu. Örneğin, Culik ve Yu, bazen Culik-Yu sınıfları olarak adlandırılan, iyi tanımlanmış üç sınıf (ve bunlardan hiçbiriyle eşleşmeyen otomatlar için dördüncü bir sınıf) önerdi; bunlara üyeliğin kararsız olduğu kanıtlandı.[36][37][38] Wolfram’ın 2. sınıfı, sabit (sabit nokta) ve salınımlı (periyodik) kurallar olmak üzere iki alt gruba ayrılabilir.[39]
4 sınıf dinamik sistem olduğu fikri aslen Nobel ödüllü kimyager Ilya Prigogine’den geldi ve bu 4 termodinamik sistem sınıfını tanımladı – (1) termodinamik dengedeki sistemler, (2) uzamsal/zamansal olarak tekdüze sistemler, (3) kaotik sistemler ve (4) tüketen yapılara sahip karmaşık dengeden uzak sistemler (bkz. Nicolis’in makalesindeki (Prigogine’in öğrencisi) şekil 1).[40]
Tersine çevrilebilir
Hücresel otomatın mevcut her konfigürasyonu için, tam olarak bir geçmiş konfigürasyon (ön görüntü) varsa, hücresel otomat tersine çevrilebilir.[41] Bir hücresel otomat, konfigürasyonları konfigürasyonlara eşleyen bir fonksiyon olarak düşünülürse, tersine çevrilebilirlik, bu fonksiyonun birebir olduğunu ima eder.[41] Hücresel bir otomat tersine çevrilebilirse, zaman-tersine çevrilmiş davranışı da bir hücresel otomat olarak tanımlanabilir; bu gerçek, hücresel otomatların topolojik bir karakterizasyonu olan Curtis-Hedlund-Lyndon teoreminin bir sonucudur.[42][43] Her konfigürasyonun bir ön görüntüsü olmadığı hücresel otomatlar için, ön görüntüleri olmayan konfigürasyonlara Garden of Eden modelleri denir.[44]
Tek boyutlu hücresel otomatlar için, bir kuralın geri alınıp alınamayacağına karar vermek için bilinen algoritmalar vardır.[45][46] Bununla birlikte, iki veya daha fazla boyutlu hücresel otomatlar için tersine çevrilebilirlik karar verilemez; yani, bir otomat kuralını girdi olarak alan ve otomatın tersine çevrilebilir olup olmadığını doğru bir şekilde belirlemesi garanti edilen bir algoritma yoktur. Jarkko Kari’nin ispatı, Wang karolarının döşeme problemi ile ilgilidir.[47]
Termodinamiğin yasalarına uyduklarından, tersinir hücresel otomatlar genellikle gaz ve sıvı dinamiği gibi fiziksel olayları simüle etmek için kullanılır. Bu tür hücresel otomatlar, tersine çevrilebilir olacak şekilde özel olarak oluşturulmuş kurallara sahiptir. Bu tür sistemler Tommaso Toffoli, Norman Margolus ve diğerleri tarafından incelenmiştir. Bilinen tersleri olan tersine çevrilebilir hücresel otomataları açıkça inşa etmek için çeşitli teknikler kullanılabilir. İki yaygın olanı, her ikisi de bir hücresel otomatın tanımını bir şekilde değiştirmeyi içeren ikinci dereceden hücresel otomat ve blok hücresel otomattır. Bu tür otomatlar, yukarıda verilen tanımı tam olarak karşılamasa da, yeterince büyük komşuluklara ve durum sayısına sahip geleneksel hücresel otomatlar tarafından taklit edilebildikleri ve dolayısıyla geleneksel hücresel otomatların bir alt kümesi olarak değerlendirilebilecekleri gösterilebilir. Tersine, her tersine çevrilebilir hücresel otomatın bir blok hücresel otomat tarafından taklit edilebileceği gösterilmiştir.[48][49]
Bütünsel
Hücresel otomatların özel bir sınıfı, bütüncül hücresel otomatlardır. Bütüncül bir hücresel otomattaki her bir hücrenin durumu bir sayı ile temsil edilir (genellikle sonlu bir kümeden alınan bir tamsayı değeri) ve bir hücrenin t zamanındaki değeri yalnızca çevresindeki hücrelerin değerlerinin toplamına bağlıdır. (muhtemelen hücrenin kendisi dahil) t – 1 zamanında.[50][51] Hücrenin t zamanındaki durumu hem kendi durumuna hem de t – 1 zamanındaki komşularının toplamına bağlıysa, hücresel otomat uygun şekilde dış bütünsel olarak adlandırılır.[51] Conway’in Game of Life, hücre değerleri 0 ve 1 olan bir dış bütünsel hücresel otomatın bir örneğidir; Life ile aynı Moore mahalle yapısına sahip dış bütünsel hücresel otomatlara bazen hayata benzer hücresel otomatlar denir.[52][53]
İlgili otomatlar
Hücresel otomat kavramının birçok olası genellemesi vardır.
Bunun bir yolu, dikdörtgen (kübik vb.) ızgaradan başka bir şey kullanmaktır. Örneğin, bir düzlem düzgün altıgenlerle döşenmişse, bu altıgenler hücre olarak kullanılabilir. Çoğu durumda, ortaya çıkan hücresel otomatlar, özel olarak tasarlanmış komşuluklara ve kurallara sahip dikdörtgen ızgaralara eşdeğerdir. Başka bir varyasyon, Penrose karolarında olduğu gibi ızgaranın kendisini düzensiz hale getirmek olabilir.[54]
Ayrıca, kurallar deterministik olmaktan çok olasılıksal olabilir. Bu tür hücresel otomatlara olasılıksal hücresel otomatlar denir. Bir olasılık kuralı, t zamanındaki her model için, merkezi hücrenin t + 1 zamanında her bir olası duruma geçiş yapma olasılıklarını verir. Bazen daha basit bir kural kullanılır; örneğin: “Kural Hayat Oyunudur, ancak her zaman adımında her hücrenin zıt renge dönüşme olasılığı %0,001’dir.”
Mahalle veya kurallar zaman veya mekan içinde değişebilir. Örneğin, başlangıçta bir hücrenin yeni durumu yatay olarak bitişik hücreler tarafından belirlenebilir, ancak sonraki nesil için dikey hücreler kullanılacaktır.
Hücresel otomatlarda, bir hücrenin yeni durumu, diğer hücrelerin yeni durumundan etkilenmez. Bu, örneğin 2’ye 2’lik bir hücre bloğunun kendisi ve kendisine bitişik hücreler tarafından belirlenebilmesi için değiştirilebilir.
Sürekli otomatlar var. Bunlar bütünsel hücresel otomatlara benzer, ancak kural ve durumların ayrı olması yerine (örneğin, {0,1,2} durumlarını kullanan bir tablo), sürekli işlevler kullanılır ve durumlar sürekli hale gelir (genellikle [0,1’deki değerler) ]). Bir konumun durumu, sonlu sayıda gerçek sayıdır. Bazı hücresel otomatlar, bu şekilde sıvı modellerinde difüzyon sağlayabilir.
Sürekli uzamsal otomatlar, konumların sürekliliğine sahiptir. Bir konumun durumu, sonlu sayıda gerçek sayıdır. Zaman da süreklidir ve durum diferansiyel denklemlere göre gelişir. Önemli bir örnek, reaksiyon-difüzyon dokuları, Alan Turing tarafından kimyasal reaksiyonların zebralar üzerinde şeritler ve leoparlar üzerinde noktalar oluşturabileceğini açıklamak için önerdiği diferansiyel denklemlerdir.[55] Bunlara hücresel otomatlar tarafından yaklaşıldığında, genellikle benzer modeller verirler. MacLennan [1], sürekli uzamsal otomatları bir hesaplama modeli olarak ele alır.
Game of Life’daki planörlere benzer yayılma fenomeni sergileyen, sürekli uzamsal otomatların bilinen örnekleri vardır.[56]
Grafik yeniden yazma otomatları, grafik yeniden yazma sistemlerine dayalı hücresel otomatların uzantılarıdır.[57]
Temel hücresel otomatlar
Önemsiz olmayan en basit hücresel otomat, hücre başına iki olası durum ve bir hücrenin komşuları hücrenin her iki yanındaki bitişik hücreler olarak tanımlanan tek boyutlu olacaktır. Bir hücre ve onun iki komşusu 3 hücrelik bir komşuluk oluşturur, dolayısıyla bir komşuluk için 2 üzeri 3 = 8 olası örüntü vardır. Bir kural, her model için hücrenin bir sonraki nesilde 1 mi yoksa 0 mı olacağına karar vermekten oluşur. O halde 2 üzeri 8 = 256 olası kural vardır.[6]
Bu 256 hücresel otomata genellikle Wolfram tarafından icat edilen ve her kurala 0 ile 255 arasında bir sayı veren standart bir adlandırma kuralı olan Wolfram koduyla anılır. Bir dizi makale bu 256 hücresel otomatı analiz etmiş ve karşılaştırmıştır. Kural 30, kural 90, kural 110 ve kural 184 hücresel otomatlar özellikle ilgi çekicidir.
Kural alanı
Bir temel hücresel otomat kuralı 8 bit ile belirtilir ve tüm temel hücresel otomat kurallarının 8 boyutlu birim hiperküpün köşelerinde oturduğu düşünülebilir. Bu birim hiperküp, hücresel otomat kural uzayıdır. Bir sonraki en yakın hücresel otomata için, bir kural 25 = 32 bit ile belirtilir ve hücresel otomat kural alanı 32 boyutlu bir birim hiperküptür. İki kural arasındaki mesafe, hiperküpün kenarı boyunca birinci kuralı temsil eden bir tepe noktasından ve başka bir kuralı temsil eden başka bir tepe noktasından hareket etmek için gereken adım sayısıyla tanımlanabilir. Bu kuraldan kurala mesafe, Hamming mesafesi olarak da adlandırılır.
Hücresel otomat kural alanı, benzer dinamik davranışa sahip kuralların birbirine “yakın” olup olmadığıyla ilgili soruyu sormamızı sağlar. 2 boyutlu düzlemde yüksek boyutlu bir hiperküpü grafiksel olarak çizmek zor bir görev olmaya devam ediyor ve hiperküpteki bir kuralın ham konumlandırıcısı, temel kurallar için 8 bitlik dizideki (veya için 32 bitlik dizideki) bit-1 sayısıdır. sonraki en yakın komşu kuralları). Kural uzayının bu dilimlerinde farklı Wolfram sınıflarındaki kuralların çizilmesi, 1. sınıf kuralların daha az sayıda bit-1’e sahip olma eğiliminde olduğunu, dolayısıyla uzayın bir bölgesinde yer aldığını, oysa 3. sınıf kuralların daha yüksek orana (% 50) sahip olma eğiliminde olduğunu göstermektedir. ) bit-1’ler.[39]
Daha büyük hücresel otomat kural uzayı için, 4. sınıf kurallarının 1. sınıf ve 3. sınıf kuralları arasında yer aldığı gösterilmiştir.[60] Bu gözlem, kaosun eşiği ifadesinin temelidir ve termodinamikteki faz geçişini anımsatır.
Uygulamalar
Biyoloji
Hücresel otomatlar tarafından birkaç biyolojik süreç meydana gelir veya simüle edilebilir.
Basit bir durum uzayı ile hücresel otomatlar tarafından modellenen bazı biyolojik olay örnekleri şunlardır:
Conus ve Cymbiola cinslerindekiler gibi bazı deniz kabuklarının desenleri, doğal hücresel otomatlar tarafından üretilir. Pigment hücreleri, kabuğun dudağı boyunca dar bir bantta bulunur. Her hücre, matematiksel bir kuralın doğal bir versiyonuna uyarak, komşu pigment hücrelerinin aktive edici ve inhibe edici aktivitesine göre pigmentler salgılar.[61] Hücre bandı, yavaş büyürken kabukta renkli desen bırakır. Örneğin, yaygın tür olan Conus tekstili, Wolfram’ın kural 30 hücresel otomatına benzeyen bir model taşır.[61]
Bitkiler, hücresel bir otomat mekanizması aracılığıyla gaz alımını ve kaybını düzenler. Yaprak üzerindeki her stoma bir hücre görevi görür.[62]
Kafadanbacaklıların derisindeki hareketli dalga modelleri, her biri genişletilmiş veya geri çekilmiş bir kromatofora karşılık gelen iki durumlu, iki boyutlu bir hücresel otomata ile simüle edilebilir.[63]
Eşik otomatları, nöronları simüle etmek için icat edildi ve tanıma ve öğrenme gibi karmaşık davranışlar simüle edilebilir.[64]
Fibroblastlar, hücresel otomata benzerlikler taşır, çünkü her bir fibroblast yalnızca komşularıyla etkileşime girer.[65]
Ek olarak, ajanların hızlarının açık bir şekilde modellenmesini gerektiren biyolojik fenomenler (örneğin, toplu hücre göçüne dahil olanlar), biyolojik kafes-gaz hücresel otomatları gibi daha karmaşık bir durum uzayı ve kuralları olan hücresel otomatlar tarafından modellenebilir. Bunlar, aşağıdakiler gibi büyük tıbbi öneme sahip fenomenleri içerir:
Metastatik invazyonun farklı modlarının karakterizasyonu.[66]
Agresif karsinomların gelişiminde heterojenliğin rolü.[67]
Tümör proliferasyonu sırasında fenotipik geçiş.[68]
Kimya
Belousov-Zhabotinsky reaksiyonu, hücresel bir otomat aracılığıyla simüle edilebilen uzay-zamansal bir kimyasal osilatördür. 1950’lerde A. M. Zhabotinsky (B. P. Belousov’un çalışmalarını genişleterek), malonik asit, asitleştirilmiş bromat ve bir serik tuzu karışımından oluşan ince, homojen bir tabakanın birbirine karıştırıldığında ve bozulmadan bırakıldığında, eşmerkezli daireler ve spiraller ortam boyunca yayılır. Scientific American’ın Ağustos 1988 sayısının “Computer Recreations” bölümünde[69] A. K. Dewdney, Bielefeld Üniversitesi’nden (Almanya) Martin Gerhardt ve Heike Schuster tarafından geliştirilen bir hücresel otomatı[70] tartıştı. Bu otomat, Belousov-Zhabotinsky reaksiyonundakilere benzeyen dalga modelleri üretir.
Fizik
Olasılıksal hücresel otomatlar, akışkan dinamiği ve faz geçişleri gibi olguları incelemek için istatistiksel ve yoğun madde fiziğinde kullanılır. Ising modeli, her bir hücrenin “yukarı” ve “aşağı” olarak adlandırılan iki durumdan birinde olabileceği ve bir mıknatısın idealleştirilmiş bir temsilini oluşturduğu prototip bir örnektir. Modelin parametrelerini ayarlayarak, aynı durumda olan hücrelerin oranı, ferromanyetlerin ısıtıldığında nasıl manyetikliği giderildiğini açıklamaya yardımcı olacak şekilde değiştirilebilir. Ayrıca, demanyetizasyon faz geçişinin incelenmesinden elde edilen sonuçlar, bir sıvının gaza buharlaşması gibi diğer faz geçişlerine aktarılabilir; bu uygun çapraz uygulanabilirlik, evrensellik olarak bilinir.[71][72] İki boyutlu Ising modelindeki ve evrensellik sınıfındaki diğer sistemlerdeki faz geçişi, derinlemesine anlamak için uyumlu alan teorisi gerektirdiğinden, özellikle ilgi çekici olmuştur.[73] Fizikte önemli olan diğer hücresel otomatlar, sıvı akışlarını simüle eden kafes gaz otomatalarını içerir.
Bilgisayar bilimi, kodlama ve iletişim
Hücresel otomat işlemciler, bilgileri hesaplamalı olarak işleyebilen CA kavramlarının fiziksel uygulamalarıdır. İşleme elemanları, özdeş hücrelerin düzenli bir ızgarasında düzenlenir. Izgara genellikle iki veya üç boyutlu bir kare döşeme veya mozaiklemedir; diğer döşemeler mümkündür, ancak henüz kullanılmamıştır. Hücre durumları yalnızca bitişik komşu hücrelerle etkileşimlerle belirlenir. Daha uzaktaki hücrelerle doğrudan iletişim kurmanın hiçbir yolu yoktur.[74] Böyle bir hücresel otomat işlemci dizisi konfigürasyonu, sistolik dizidir. Hücre etkileşimi, elektrik yükü, manyetizma, titreşim (kuantum ölçeğinde fononlar) veya fiziksel olarak yararlı başka herhangi bir araç aracılığıyla olabilir. Bu, herhangi bir eleman arasında kabloya ihtiyaç duyulmayacak şekilde birkaç şekilde yapılabilir. Bu, günümüzde çoğu bilgisayarda kullanılan (von Neumann tasarımları) işlemcilerden çok farklıdır ve teller üzerinden uzaktaki öğelerle iletişim kurabilen öğelerle bölümlere ayrılmıştır.
Kural 30, başlangıçta kriptografide kullanım için olası bir blok şifre olarak önerildi. İki boyutlu hücresel otomata, sahte bir sayı üreteci oluşturmak için kullanılabilir.[75]
Açık anahtarlı kriptografi için hücresel otomatlar önerilmiştir. Tek yönlü fonksiyon, tersinin bulunmasının zor olduğuna inanılan sonlu bir CA’nın evrimidir. Kural göz önüne alındığında, herkes gelecekteki durumları kolayca hesaplayabilir, ancak önceki durumları hesaplamak çok zor görünmektedir. Hata düzeltme kodlarını tasarlamak için hücresel otomatlar da uygulanmıştır.[76]
Hücresel otomata ile çözülebilecek diğer problemler şunları içerir:
Ateş mangası senkronizasyon sorunu
Çoğunluk sorunu
Üretken sanat ve müzik
Hücresel otomatlar, üretken müzikte[77] ve evrimsel müzik kompozisyonunda[78] ve video oyunlarında prosedürel arazi üretiminde kullanılmıştır.[79]
Belirli hücresel otomata kuralları şunları içerir:
Brian’s Brain
Codd’s cellular automaton
CoDi
Conway’s game of life
Day and Night
Langton’s ant
Langton’s loops
Nobili cellular automata
Rule 90
Rule 184
Seeds
Turmite
Von Neumann cellular automaton
Wireworld
1970’de İngiliz matematikçi Horton Conway tarafından geliştirilen bir hücresel otomat olan Hayat Oyunu’nda “planör” oluşumunu gösteren bir animasyon.

Kırmızı hücreler, mavi hücre için Moore mahallesidir.
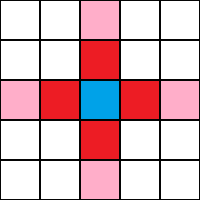
Kırmızı hücreler, mavi hücre için von Neumann mahallesidir. Menzil-2 “çapraz komşuluk” pembe hücreleri de içerir.
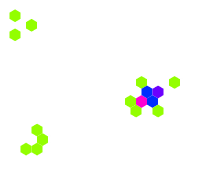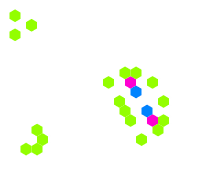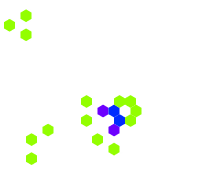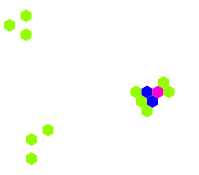
Kareler yerine altıgen hücrelere dayalı bir hücresel otomat (kural 34/2)
Kaynaklar:
https://en.wikipedia.org/wiki/Cellular_automaton
https://en.wikipedia.org/wiki/File:Gospers_glider_gun.gif
https://en.wikipedia.org/wiki/File:CA-Moore.svg
https://en.wikipedia.org/wiki/File:CA-von-Neumann.svg
https://en.wikipedia.org/wiki/File:Oscillator.gif
Wiki Notlar:
1)Daniel Dennett (1995), Darwin’s Dangerous Idea, Penguin Books, London, ISBN 978-0-14-016734-4, ISBN 0-14-016734-X
2)Wolfram, Stephen (1983). “Statistical Mechanics of Cellular Automata”. Reviews of Modern Physics. 55 (3): 601–644. Bibcode:1983RvMP…55..601W. doi:10.1103/RevModPhys.55.601. Archived from the original on 21 September 2013. Retrieved 28 February 2011.
3)Toffoli, Tommaso; Margolus, Norman (1987). Cellular Automata Machines: A New Environment for Modeling. MIT Press. p. 27. ISBN 9780262200608.
4)Schiff, Joel L. (2011). Cellular Automata: A Discrete View of the World. Wiley & Sons, Inc. p. 40. ISBN 9781118030639.
5)Kier, Seybold, Cheng 2005, p. 15
6)Bialynicki-Birula, Bialynicka-Birula 2004, p. 9
7)Schiff 2011, p. 41
8)Pickover, Clifford A. (2009). The Math Book: From Pythagoras to the 57th Dimension, 250 Milestones in the History of Mathematics. Sterling Publishing Company, Inc. p. 406. ISBN 978-1402757969.
9)Schiff 2011, p. 1
10)John von Neumann, “The general and logical theory of automata,” in L.A. Jeffress, ed., Cerebral Mechanisms in Behavior – The Hixon Symposium, John Wiley & Sons, New York, 1951, pp. 1–31.
11)Kemeny, John G. (1955). “Man viewed as a machine”. Sci. Am. 192 (4): 58–67. Bibcode:1955SciAm.192d..58K. doi:10.1038/scientificamerican0455-58.; Sci. Am. 1955; 192:6 (errata).
12)Schiff 2011, p. 3
13)Ilachinski 2001, p. xxix
14)Bialynicki-Birula, Bialynicka-Birula 2004, p. 8
15)Wolfram 2002, p. 876
16)von Neumann, John; Burks, Arthur W. (1966). Theory of Self-Reproducing Automata. University of Illinois Press.
17)Wiener, N.; Rosenblueth, A. (1946). “The mathematical formulation of the problem of conduction of impulses in a network of connected excitable elements, specifically in cardiac muscle”. Arch. Inst. Cardiol. México. 16 (3): 205–65. PMID 20245817.
18)Letichevskii, A. A.; Reshodko, L. V. (1974). “N. Wiener’s theory of the activity of excitable media”. Cybernetics. 8 (5): 856–864. doi:10.1007/bf01068458. S2CID 121306408.
19)Davidenko, J. M.; Pertsov, A. V.; Salomonsz, R.; Baxter, W.; Jalife, J. (1992). “Stationary and drifting spiral waves of excitation in isolated cardiac muscle”. Nature. 355 (6358): 349–351. Bibcode:1992Natur.355..349D. doi:10.1038/355349a0. PMID 1731248. S2CID 4348759.
20)Hedlund, G. A. (1969). “Endomorphisms and automorphisms of the shift dynamical system”. Math. Systems Theory. 3 (4): 320–3751. doi:10.1007/BF01691062. S2CID 21803927.
21)Schiff 2011, p. 182
22)Smith, Alvy Ray. “Cellular Automata Complexity Trade-Offs” (PDF).
23)Smith, Alvy Ray. “Simple Computation-Universal Cellular Spaces” (PDF).
24)Smith, Alvy Ray. “Simple Nontrivial Self-Reproducing Machines” (PDF).
25)Smith, Alvy Ray. “Introduction to and Survey of Cellular Automata or Polyautomata Theory” (PDF).
26)Gardner, Martin (1970). “Mathematical Games: The fantastic combinations of John Conway’s new solitaire game “life””. Scientific American. 223 (4): 120–123. doi:10.1038/scientificamerican1070-120.
27)Paul Chapman. Life universal computer. http://www.igblan.free-online.co.uk/igblan/ca/ November 2002
28)Wainwright 2010, p. 16
29)Wolfram 2002, p. 880
30)Wolfram 2002, p. 881
31)Mitchell, Melanie (4 October 2002). “Is the Universe a Universal Computer?”. Science. 298 (5591): 65–68. doi:10.1126/science.1075073. S2CID 122484855.
32)Ilachinsky 2001, p. 12
33)Ilachinsky 2001, p. 13
34)Wolfram 2002, p. 231
35)Zenil, Hector (2010). “Compression-based investigation of the dynamical properties of cellular automata and other systems” (PDF). Complex Systems. 19 (1): 1–28. doi:10.25088/ComplexSystems.19.1.1. S2CID 15364755.
36)G. Cattaneo; E. Formenti; L. Margara (1998). “Topological chaos and CA”. In M. Delorme; J. Mazoyer (eds.). Cellular automata: a parallel model. Springer. p. 239. ISBN 978-0-7923-5493-2.
37)Burton H. Voorhees (1996). Computational analysis of one-dimensional cellular automata. World Scientific. p. 8. ISBN 978-981-02-2221-5.
38)Max Garzon (1995). Models of massive parallelism: analysis of cellular automata and neural networks. Springer. p. 149. ISBN 978-3-540-56149-1.
39)Li, Wentian; Packard, Norman (1990). “The structure of the elementary cellular automata rule space” (PDF). Complex Systems. 4: 281–297. Retrieved 25 January 2013.
40)Nicolis (1974). “Dissipative Structures, Catastrophes, and Pattern Formation: A Bifurcation Analysis” (PDF). PNAS. 71 (7): 2748–2751. Bibcode:1974PNAS…71.2748N. doi:10.1073/pnas.71.7.2748. PMC 388547. PMID 16592170. Retrieved 25 March 2017.
41)Kari, Jarrko 1991, p. 379
42)Richardson, D. (1972). “Tessellations with local transformations”. J. Comput. Syst. Sci. 6 (5): 373–388. doi:10.1016/S0022-0000(72)80009-6.
43)Margenstern, Maurice (2007). Cellular Automata in Hyperbolic Spaces – Tome I, Volume 1. Archives contemporaines. p. 134. ISBN 978-2-84703-033-4.
44)Schiff 2011, p. 103
45)Amoroso, Serafino; Patt, Yale N. (1972). “Decision Procedures for Surjectivity and Injectivity of Parallel Maps for Tessellation Structures”. J. Comput. Syst. Sci. 6 (5): 448–464. doi:10.1016/s0022-0000(72)80013-8.
46)Sutner, Klaus (1991). “De Bruijn Graphs and Linear Cellular Automata” (PDF). Complex Systems. 5: 19–30.
47)Kari, Jarkko (1990). “Reversibility of 2D cellular automata is undecidable”. Physica D. 45 (1–3): 379–385. Bibcode:1990PhyD…45..379K. doi:10.1016/0167-2789(90)90195-U.
48)Kari, Jarkko (1999). “On the circuit depth of structurally reversible cellular automata”. Fundamenta Informaticae. 38: 93–107. doi:10.3233/FI-1999-381208.
49)Durand-Lose, Jérôme (2001). “Representing reversible cellular automata with reversible block cellular automata”. Discrete Mathematics and Theoretical Computer Science. AA: 145–154. Archived from the original on 15 May 2011.
50)Wolfram 2002, p. 60
51)Ilachinski, Andrew (2001). Cellular automata: a discrete universe. World Scientific. pp. 44–45. ISBN 978-981-238-183-5.
52)The phrase “life-like cellular automaton” dates back at least to Barral, Chaté & Manneville (1992), who used it in a broader sense to refer to outer totalistic automata, not necessarily of two dimensions. The more specific meaning given here was used e.g. in several chapters of Adamatzky (2010). See: Barral, Bernard; Chaté, Hugues; Manneville, Paul (1992). “Collective behaviors in a family of high-dimensional cellular automata”. Physics Letters A. 163 (4): 279–285. Bibcode:1992PhLA..163..279B. doi:10.1016/0375-9601(92)91013-H.
53)Eppstein 2010, pp. 72–73
54)Jacob Aron. “First gliders navigate ever-changing Penrose universe”. New Scientist.
55)Murray, J. D. (2003). Mathematical biology (3rd ed.). New York: Springer. ISBN 0-387-95228-4.
56)Pivato, M: “RealLife: The continuum limit of Larger than Life cellular automata”, Theoretical Computer Science, 372 (1), March 2007, pp. 46–68
57)Tomita, Kohji; Kurokawa, Haruhisa; Murata, Satoshi (2009). “Graph-Rewriting Automata as a Natural Extension of Cellular Automata”. Adaptive Networks. Understanding Complex Systems. pp. 291–309. doi:10.1007/978-3-642-01284-6_14. ISBN 978-3-642-01283-9.
58)Giles, Jim (2002). “What Kind of Science is This?”. Nature. 417 (6886): 216–218. Bibcode:2002Natur.417..216G. doi:10.1038/417216a. PMID 12015565. S2CID 10636328.
59)Weinberg, Steven (24 October 2002). “Is the Universe a Computer?”. The New York Review of Books. Retrieved 12 October 2012.
60)Wentian Li; Norman Packard; Chris G Langton (1990). “Transition phenomena in cellular automata rule space”. Physica D. 45 (1–3): 77–94. Bibcode:1990PhyD…45…77L. CiteSeerX 10.1.1.15.2786. doi:10.1016/0167-2789(90)90175-O.
61)Coombs, Stephen (15 February 2009), The Geometry and Pigmentation of Seashells (PDF), pp. 3–4, archived from the original (PDF) on 7 January 2013, retrieved 2 September 2012
62)Peak, West; Messinger, Mott (2004). “Evidence for complex, collective dynamics and emergent, distributed computation in plants”. Proceedings of the National Academy of Sciences. 101 (4): 918–922. Bibcode:2004PNAS..101..918P. doi:10.1073/pnas.0307811100. PMC 327117. PMID 14732685.
63)”Archived copy” (PDF). Archived from the original (PDF) on 25 July 2010. Retrieved 14 September 2008.
64)Ilachinsky 2001, p. 275
65)Yves Bouligand (1986). Disordered Systems and Biological Organization. pp. 374–375.
66)Ilina, Olga; Gritsenko, Pavlo G.; Syga, Simon; Lippoldt, Jürgen; La Porta, Caterina A. M.; Chepizhko, Oleksandr; Grosser, Steffen; Vullings, Manon; Bakker, Gert-Jan; Starruß, Jörn; Bult, Peter (September 2020). “Cell–cell adhesion and 3D matrix confinement determine jamming transitions in breast cancer invasion”. Nature Cell Biology. 22 (9): 1103–1115. doi:10.1038/s41556-020-0552-6. ISSN 1465-7392. PMC 7502685. PMID 32839548.
67)Reher, David; Klink, Barbara; Deutsch, Andreas; Voss-Böhme, Anja (11 August 2017). “Cell adhesion heterogeneity reinforces tumour cell dissemination: novel insights from a mathematical model”. Biology Direct. 12 (1): 18. doi:10.1186/s13062-017-0188-z. ISSN 1745-6150. PMC 5553611. PMID 28800767.
68)Hatzikirou, H.; Basanta, D.; Simon, M.; Schaller, K.; Deutsch, A. (1 March 2012). “‘Go or Grow’: the key to the emergence of invasion in tumour progression?”. Mathematical Medicine and Biology. 29 (1): 49–65. doi:10.1093/imammb/dqq011. ISSN 1477-8599. PMID 20610469.
69)A. K. Dewdney, The hodgepodge machine makes waves, Scientific American, p. 104, August 1988.
70)Gerhardt, M.; Schuster, H. (1989). “A cellular automaton describing the formation of spatially ordered structures in chemical systems”. Physica D. 36 (3): 209–221. Bibcode:1989PhyD…36..209G. doi:10.1016/0167-2789(89)90081-x.
71)Sethna, James P. (2008). Statistical Mechanics: Entropy, Order Parameters, and Complexity. Oxford University Press. ISBN 978-0-198-56677-9. OCLC 845714772.
72)Kardar, Mehran (2007). Statistical Physics of Fields. Cambridge University Press. ISBN 978-0-521-87341-3. OCLC 920137477.
73)Cappelli, Andrea; Zuber, Jean-Bernard (2010). “A-D-E Classification of Conformal Field Theories”. Scholarpedia. 5 (4): 10314. arXiv:0911.3242. Bibcode:2010SchpJ…510314C. doi:10.4249/scholarpedia.10314. S2CID 18207779.
74)Muhtaroglu, Ali (August 1996). “4.1 Cellular Automaton Processor (CAP)”. Cellular Automaton Processor Based Systems for Genetic Sequence Comparison/Database Searching. Cornell University. pp. 62–74.
75)Tomassini, M.; Sipper, M.; Perrenoud, M. (2000). “On the generation of high-quality random numbers by two-dimensional cellular automata”. IEEE Transactions on Computers. 49 (10): 1146–1151. doi:10.1109/12.888056.
76)Chowdhury, D. Roy; Basu, S.; Gupta, I. Sen; Chaudhuri, P. Pal (June 1994). “Design of CAECC – cellular automata based error correcting code”. IEEE Transactions on Computers. 43 (6): 759–764. doi:10.1109/12.286310.
77)Burraston, Dave, and Ernest Edmonds. “Cellular automata in generative electronic music and sonic art: a historical and technical review.” Digital Creativity 16.3 (2005): 165-185.
78)Miranda, Eduardo Reck. “Evolving cellular automata music: From sound synthesis to composition.” Proceedings of 2001 Workshop on Artificial Life Models for Musical Applications. 2001.
79)Ashlock, Daniel; Kreitzer, Matthew (2020). “Evolving Diverse Cellular Automata Based Level Maps”. Proceedings of 6th International Conference in Software Engineering for Defence Applications. Advances in Intelligent Systems and Computing. Vol. 925. pp. 10–23. doi:10.1007/978-3-030-14687-0_2. ISBN 978-3-030-14686-3. S2CID 85562837
Wiki Kaynaklar:
Adamatzky, Andrew, ed. (2010). Game of Life Cellular Automata. Springer. ISBN 978-1-84996-216-2.
Wainwright, Robert. “Conway’s game of life: early personal recollections”. In Adamatzky (2010).
Eppstein, David. “Growth and decay in life-like celular autometa”. In Adamatzky (2010).
Bialynicki-Birula, Iwo; Bialynicka-Birula, Iwona (2004). Modeling Reality: How Computers Mirror Life. Oxford University Press. ISBN 978-0198531005.
Chopard, Bastien; Droz, Michel (2005). Cellular Automata Modeling of Physical Systems. Cambridge University Press. ISBN 978-0-521-46168-9.
Gutowitz, Howard, ed. (1991). Cellular Automata: Theory and Experiment. MIT Press. ISBN 9780262570862.
Ilachinski, Andrew (2001). Cellular Automata: A Discrete Universe. World Scientific. ISBN 9789812381835.
Kier, Lemont B.; Seybold, Paul G.; Cheng, Chao-Kun (2005). Modeling Chemical Systems using Cellular Automata. Springer. ISBN 9781402036576.
Kroc, Jiří; Jiménez-Morales, Francisco; Guisado, José Luis; Lemos, María Carmen; Tkáč, Jakub (December 2019). “Building Efficient Computational Cellular Automata Models of Complex Systems: Background, Applications, Results, Software, and Pathologies”. Advances in Complex Systems. 22 (5): 1950013 (38 pages). doi:10.1142/S0219525919500139. S2CID 212988726.
Wolfram, Stephen (2002). A New Kind of Science. Wolfram Media. ISBN 978-1579550080.
Cellular automaton FAQ from the newsgroup comp.theory.cell-automata
“Neighbourhood Survey” (includes discussion on triangular grids, and larger neighborhood CAs)
von Neumann, John, 1966, The Theory of Self-reproducing Automata, A. Burks, ed., Univ. of Illinois Press, Urbana, IL.
Cosma Shalizi’s Cellular Automata Notebook contains an extensive list of academic and professional reference material.
Wolfram’s papers on CAs Archived 27 September 2013 at the Wayback Machine
A.M. Turing. 1952. The Chemical Basis of Morphogenesis. Phil. Trans. Royal Society, vol. B237, pp. 37–72. (proposes reaction-diffusion, a type of continuous automaton).
Evolving Cellular Automata with Genetic Algorithms: A Review of Recent Work, Melanie Mitchell, James P. Crutchfeld, Rajarshi Das (In Proceedings of the First International Conference on Evolutionary Computation and Its Applications (EvCA’96). Moscow, Russia: Russian Academy of Sciences, 1996.)
The Evolutionary Design of Collective Computation in Cellular Automata, James P. Crutchfeld, Melanie Mitchell, Rajarshi Das (In J. P. Crutch¯eld and P. K. Schuster (editors), Evolutionary Dynamics|Exploring the Interplay of Selection, Neutrality, Accident, and Function. New York: Oxford University Press, 2002.)
The Evolution of Emergent Computation, James P. Crutchfield and Melanie Mitchell (SFI Technical Report 94-03-012)
Ganguly, Sikdar, Deutsch and Chaudhuri “A Survey on Cellular Automata”




